ОПЕРАТОРИ ПРИСВОЄННЯ

ОПЕРАТОР ПРИСВОЄННЯ. СТАНДАРТНІ ФУНКЦІї.

АРИФМЕТИЧНІ ВИРАЗИ.

Зміст

Задачі

Оператор присвоєння має вигляд : < зміна >:=< вираз > ;

При його виконанні обчислюється значення виразу, що стоїть справа і присвоюється змінній, яка стоїть зліва. При цьому тип виразу повинен співпадати із типом змінної. Однак допускається присвоєння дійсним змінним цілочисельних значень.

Вирази, присутні в операторі присвоєння, можуть бути арифметичними, логічними і рядковими. Розглянемо арифметичні вирази. До їх складу входять числа, числові змінні та константи, стандартні функції, з'єднанні арифметичними операціями та круглими дужками.

Для арифметичних операцій над числовими операндами встановлена така черговість (пріоритет) виконання:

1)обчислення функцій; 2) множення (*), ділення (/), ділення націло div), остача від ділення (mod); 3) додавання (+), віднімання (-).

Для зміни порядку виконання арифметичних операцій використовують круглі дужки. Операції одного і того ж самого пріоритету виконуються зліва направо у порядку їх появи у виразі.

Функції, що входять до арифметичних виразів, називаються чисельними функціями. До аргументів цілого та дійсного типів можуть застосовуватись такі чисельні стандартні функції:

Ім'я функції, тип аргументу та результату	Математичне означення та результат
Sin(x:real):real	sin x, x в радіанах
Cos(x:real):real	cos x, x в радіанах
ArcTan (x:real):real	arctgx, значення функціїв радіанах
Pi: real	число pi=3,141592653589793
Ln(x: real): real	ln x, x>0
Exp(x: real): real
Sgrt(x: real): real
Sgr (x: real ): real
Abs(x: real): real	\|x\|
Int(x: real): real	[x] - ціла частина x
Trunc(x: real): integer	[x] - ціла частина х
Frac(x: real): real	{x} - дробова частина х
Round(x: real): integer	округлення до цілого
Random: real	випадкове число в діапазоні 0.. 0. 99
Random(i:integer):integer	випадкове число в діапазоні від 1 до i

Зауваження1. Неважко помітити, що у таблиці відсутні такі математичні функції як tg x, ctg x, arcsin x, arccos x, arcctg x, log x, та ін.

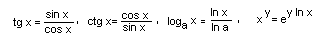
Зауваження2. Аргументи тригонометричних функцій і значення обернених тригонометричних функцій задаються в радіанах. Для переходу від градусної міри до радіанної і навпаки використовують формули.

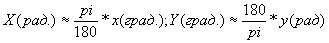
Наведемо приклади запису арифметичних виразів.

Математичний запис

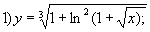
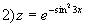
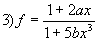
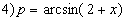
Запис на мові Паскаль

1) y:=Exp((1/3)*Ln(1+Sqr(1+Sqrt(x)))));
2) z:=Exp(-Sqr(Sin(3*x)));
3) f:= (1+2*a*x)/(1+5*b*Exp(3*Ln(x)));
4) p:=ArcTan((2+x)/Sqrt(1-Sqr(2+x)));

Зміст

Задачі